What We Do: Signal Processing with Machine Learning
When we launched Expedition Technology (EXP) in 2013, our vision of the future was not centered on a specific technology. Building a company that is
May 30, 2023
Menu
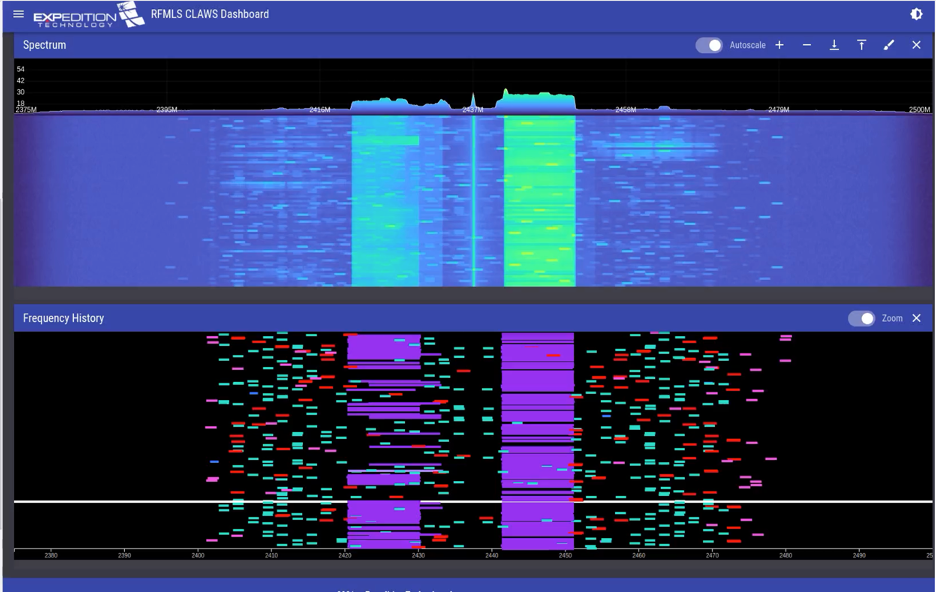
When we launched Expedition Technology (EXP) in 2013, our vision of the future was not centered on a specific technology. Building a company that is
by Aimee Moses, Kelsey O’Haire, and Chris Bogart At Expedition Technology (EXP), we ride the cutting edge of research to develop the most impactful solutions
Expedition Technology, Inc. (EXP) announces a Phase 2 Small Business Innovative Research (SBIR) award for continued development of a neural network-based technique to mitigate the effects of
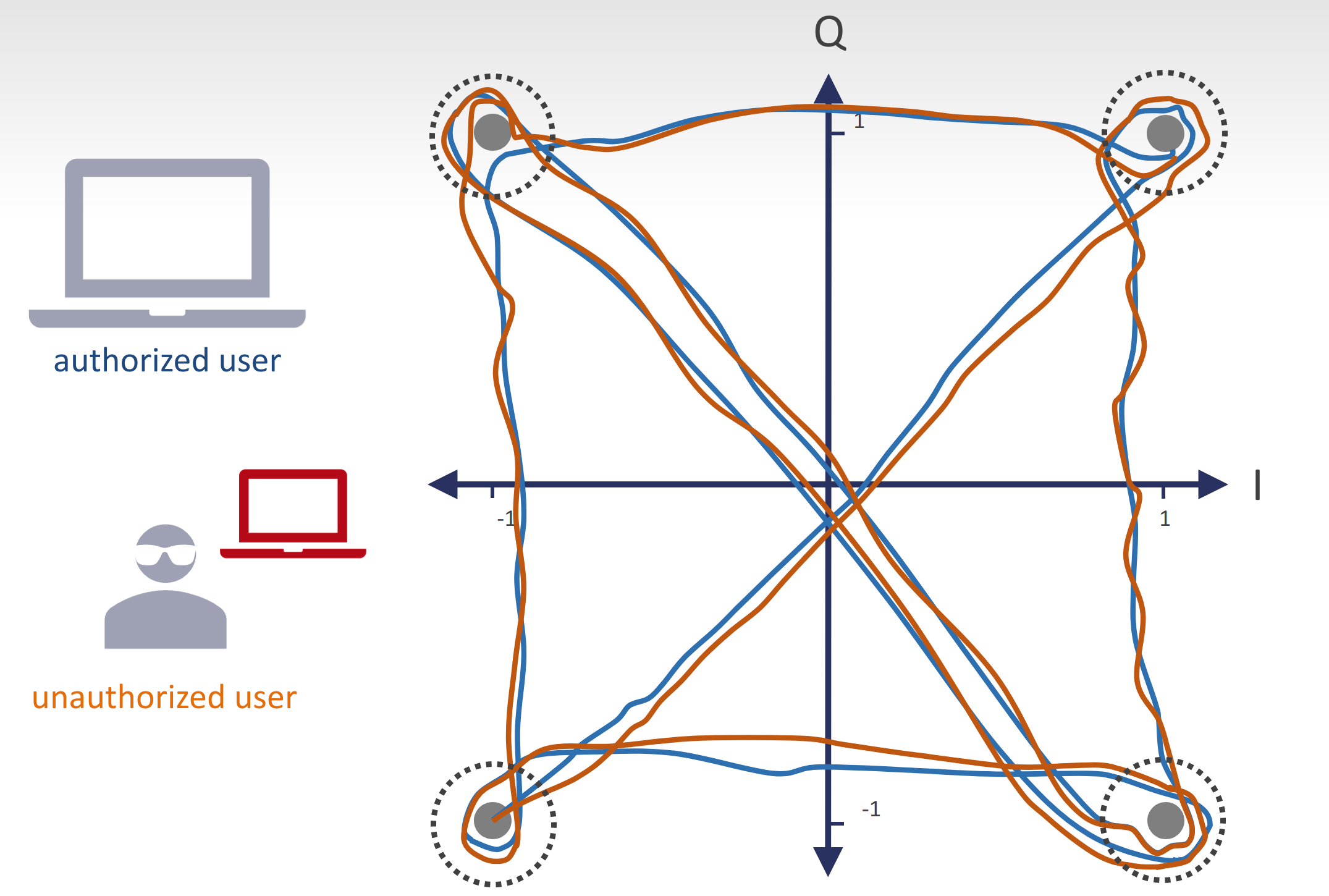
For the past five years Expedition Technology has been developing novel deep learning architectures to solve a broad set of signal processing research problems. While
Expedition Technology, Inc. (EXP) announces a Phase II Small Business Innovation Research (SBIR) award to continue the Improved Geolocation for Over the Horizon Radar (IGOR)
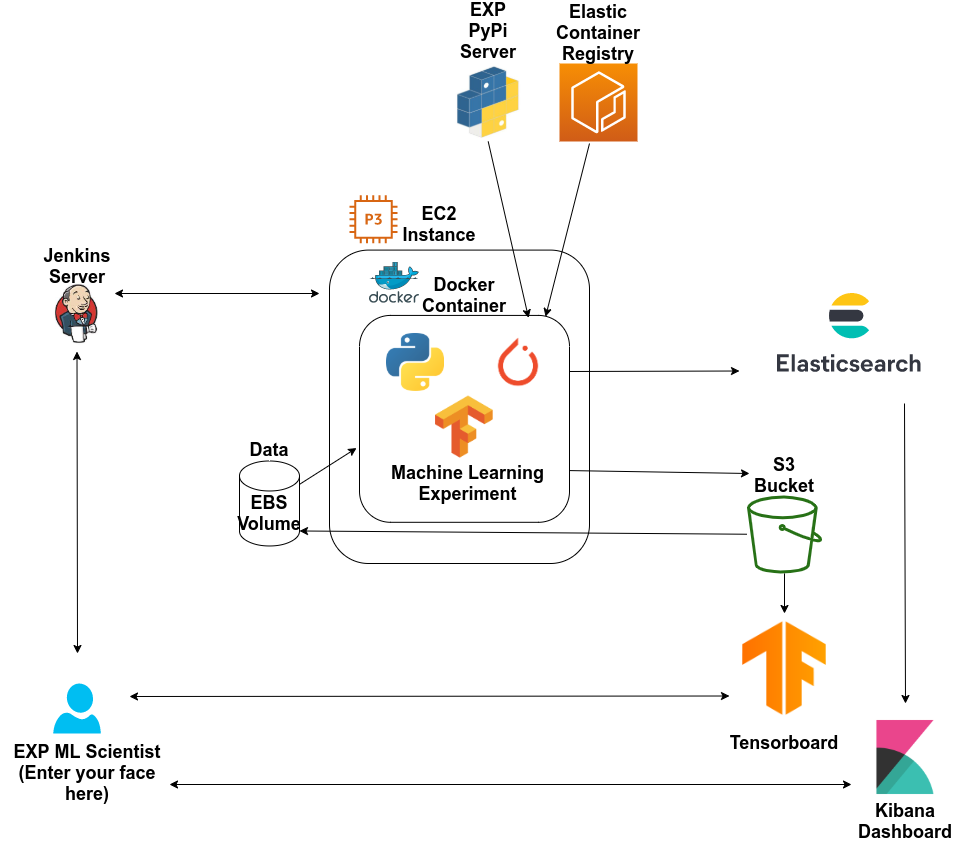
by Michael Person and Carter Brown At Expedition (EXP), we develop state of the art systems for our customers that leverage cutting edge Machine Learning
Expedition Technology, Inc. (EXP) announces a Phase 3 award to continue support to the Defense Advanced Research Projects Agency (DARPA) for the Radio Frequency Machine Learning System
Expedition Technology, Inc. (EXP) announces a $5 million, 30-month contract extension to continue 3D object detection and advanced analytic capability development for the Air Force
This summer, we hosted a group of five interns with an array of skills to match the needs of our projects as EXP grows. Their work spanned many areas including web design, Bayesian Pearl belief propagation, generative adversarial networks (GANs) for wireless data, self-supervised machine learning, and more. This blog post focuses on our interns’ experiences in their own words.
by Jesse Ranjit (ed. Andrew Draganov) About three months ago, I started my internship at Expedition Technology Inc. My short time here was loaded with
Building teams of great people who explore novel technology and deliver solutions with national impact.
© 2023 – Expedition Technology, Inc., All Rights Reserved